A/B Test Statistical Significance Calculator [Free Excel]
The statistics of A/B testing results can be confusing unless you know the exact formulas. Earlier, we had published an article on the mathematics of A/B testing and we also have a A/B test statistical significance calculator on our website to check if your results are significant or not.
The calculator provides an interface for you to calculate your A/B test’s statistical significance but does not give you the formulas used for calculating it. The article, on the other hand, provides an introduction to A/B testing statistics and talks about the math that goes behind A/B split testing and the importance of statistical significance.
Download Free: A/B Testing Guide
VWO’s A/B testing solution helped retail company Greene improve their revenue by almost 60%. However, A/B tests can be tricky to execute and interpret. So, unless you believe in predicting A/B test results using Indian astrology, this blog will tell you the math behind easy calculation of statistical significance of your tests.
The ‘what’, ‘why’ and ‘how’ of statistical significance
Before we move to complex statistical significance formulas, let’s first understand what it is, why it is important, and how to ensure that your tests conclude with statistical significance.
What is statistical significance?
Statistical significance is nothing but the probability that the gap between conversion rates of any chosen variation and the control is not because of random chance but due to a well planned, data-backed process. In this data backed process, you first gather user insights on how they are interacting with your website and then use the gathered data to formulate a scientific testing hypothesis.
Your significance level also reflects your confidence level as well as risk tolerance.
For instance, if you run an A/B test with 80% significance, while determining the winner you can be 80% confident that the results produced are not a product of any random hunch or chance. Moreover, 80% significance also reflects that there is a 20% chance that you may be wrong.
Why is statistical significance important?
For A/B testing to be successful, the test results should be statistically significant. You cannot tell for certain how future visitors will react to your website. All you can do is observe the next few visitors, record their behavior, statistically analyze it, and based on that, suggest and make changes to optimize the experience of the next users. A/B testing allows you to battle the aforementioned uncertainty and improve your website’s user experience provided each and every step is planned considering each variable in play like total website traffic, sample traffic, test duration and so on. A good example of this is Germany based company Dachfenster-rollo.de that improved their conversion rate by 33% by A/B testing their user experience.
Your marketing team’s quest for exact predictions about future visitors and the inherent uncertainty in making such predictions necessitates statistical significance. Statistical significance is also important because it serves as a source of confidence and assures you that the changes you make do have a positive impact on your business goals.
How to ensure the statistical significance of a test?
Statistical significance depends on 2 variables:
- The number of visitors, i.e your sample size.
- The number of conversions for both control and variation(s).
To ensure that your A/B tests conclude with statistical significance, plan your testing program keeping both these variables in mind. Use our free A/B test significance calculator to know your test’s significance level.
Download Free: A/B Testing Guide
How to calculate statistical significance in excel sheet with A/B testing formulas?
We have come up with a FREE spreadsheet which details exactly how to calculate statistical significance in an excel. You just need to provide the number of visitors and conversions for control and variations. The excel calculator automatically shows you the significance, p-value, z-value and other relevant metrics for any kind of A/B split testing (including Adwords). And, to add to our article on the mathematics of A/B testing and free A/B test statistical significance calculator, we share the A/B testing significance formula in excel for calculating test result significance.
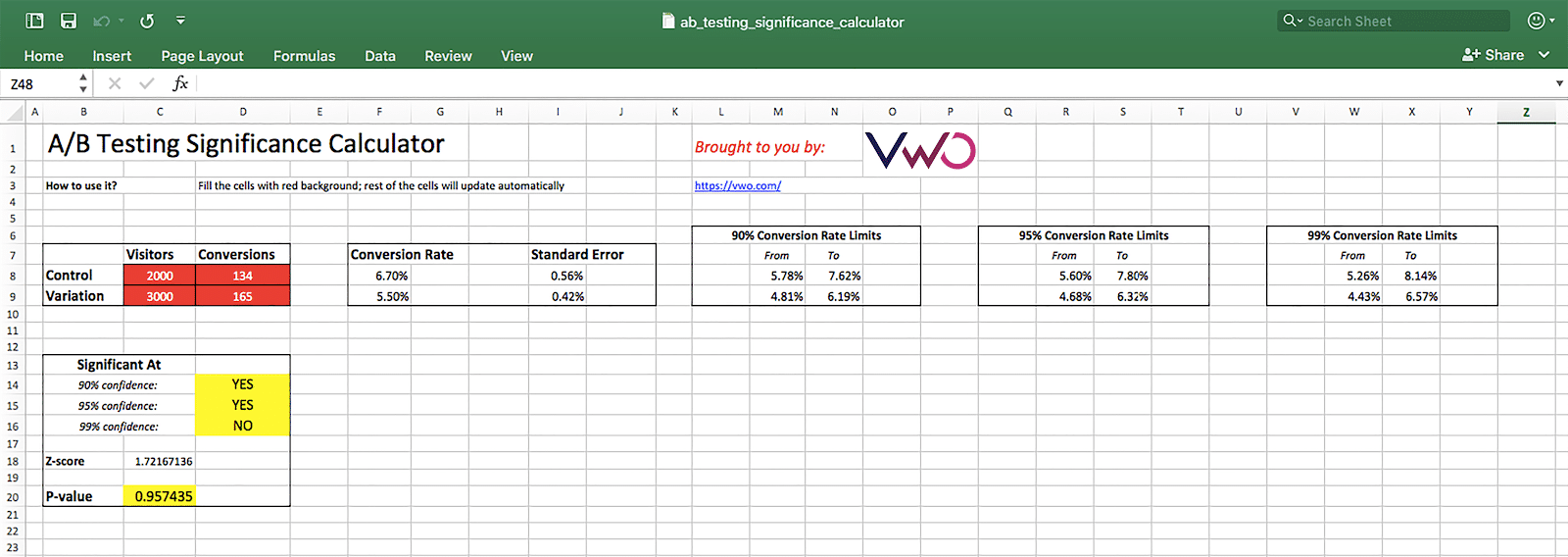
Click here to download the A/B testing significance calculator (excel sheet)
Please feel free to share the file with your friends and colleagues or post it on your blog and social media handles.
PS: By the way, if you want to do quick calculations, we have a version of this A/B testing significance calculator hosted on Google Sheets
(You will have to make a copy of the Google sheet into your own Google account before you make any changes to it).
At VWO, we believe that understanding the statistics behind A/B testing should not be your headache. Your tool should take care of this. If you’d like to try VWO SmartStats that offers intuitive and intelligent reports of your A/B tests, take a guided free trial.
Frequently asked questions
The p-value or probability value is a statistical measurement that helps determine the validity of a hypothesis based on observed data. Typically, a p-value of 0.05 or lower is commonly accepted as statistically significant, suggesting strong evidence against the null hypothesis. When the p-value is equal to or less than 0.05, it tells us that there’s good evidence against the null hypothesis and supports an alternative hypothesis.
A p-value of 0.05 indicates a commonly accepted threshold for statistical significance in an excel. This signifies that there is a 5% chance that the observed result is due to random chance and the null hypothesis is true. If the p-value is less than or equal to 0.05, it serves as an evidence against the null hypothesis and supports the alternative hypothesis. For instance, you have two data sets, A and B, and you determine the statistical difference between their means. By calculating statistical significance in an excel, you get a p-value of 0.03. With this result, you can conclude that the data gives you strong evidence to reject the null hypothesis and the significant difference between data set A and B.
Simply put, the p-value can be thought of as a “probability of chance”. It quantified the likelihood of getting the observed results by random chance, assuming that there is no actual difference between the means of two data sets. A lower p-value means that the results are less likely to be due to chance or more likely to indicate a meaningful effect.
However, the interpretation of the p-value must be considered along with other factors like sample size, test, duration, context of the research, and so on to reach statistically significant results.
While you can use the A/B testing significance formula in excel, we suggest you try our A/B test statistical significance calculator. Using this free calculator, you can get accurate calculations without spending too much time to obtain the statistical significance. In fact, you can spend the saved time on other critical activities like hypothesis formulation, test result analysis, and user behavior research. After all, why worry when you select the right tool to do the job on your behalf?












Aren’t all non-converting visitors a mistrial?
i.e., if I multiple the number of visitors by 10x, but keep the conversions the same, the statistical significance of the results should not change.
See http://blog.asmartbear.com/easy-statistics-for-adwords-ab-testing-and-hamsters.html
@Portman: No, the number of visitors in the test influence the standard deviation and hence the significance. Suppose you have 10 visitors and 2 conversions v/s 1000 visitors and 200 conversions. You have a much better idea of conversion rate in the latter than the former.
http://www.cliffsnotes.com/study_guide/Point-Estimates-and-Confidence-Intervals.topicArticleId-25951,articleId-25932.html
When you are using the values 1.65 and 1.96 to calculate significance isn’t that the niveau for 90% and 95 % respectively? At least, that’s what I take from the other website.
@Benjamin: you will notice that it is +/- 1.65 * SE so that covers the full 95% of area of normal curve.
Fail. Your Conversion rate limits overlap at the 95% level but you say that they are significant. This is inconsistant.
@Dennis: not sure if I got your point. Can you elaborate?
Sure, in your spreadsheet your 95% conversion rate limit for the control is between 5.68% and 7.62% while the conversion rate for the variation is between 4.81% and 6.89%. These two ranges overlap and thus you have failed to find a significant difference as the conversion rate may be 6% for the control and 6% for the variation.
However you have listed in another box that your conversion rate at 95% confidence is significant.
This result contradicts your 95& conversion rate limits results.
Could you please respond to the last comment posted by Dennis? It does seem your worksheet contradicts itself. I would like to use it, but I want to make sure it is accurate.
@Joe and @Dennis: actually, 95% range of conversion rate is different from being significant at 95% confidence level. If you visualize conversion rate ranges as a normal curves, then the overlap in 95% range constitutes a tiny area and that’s why the resultant z-value becomes significant at 95% confidence level.
I hope I am clear. If not, let me know. Will try to clarify.
Isn’t it because you are using 1.65 instead of 1.96? If you are doing a two-tailed test, 1.65 only gives you a 90% range. 1.96 is required for a 95% range, again on a two-tailed view. If you define it as checking if variation is better than control (pvariation-pcontrol<=0), then you could use a one tail range maybe. But it seems your calculator is just trying to show if they are different (i.e., you care if either one is larger than the other).
@Joe: Yes, you are right. It isn’t a one-tailed test. It depends on how you are interpreting the result but I am glad you clarified.
For the online version of the calculator, you set the minimum N as being 15. Does n=15 have an special relevance?
@Bartek: which N are you talking about?
Could I use this tool for evaluating responses to a survey?
E.g. 1000 respondents, 600 are satisfied, 400 are not satisfied. is the difference statistically significant?
What’s the best way to measure statistical significance of revenue improvements. I have my split test feeding data into Analytics but I’m interested in knowing at what point my Per Visit Value (which may not correlate well with raw conversions) becomes statistically relevant. Is their a way of calculating this? To me, the answer isn’t at what point the number of conversions becomes statistically relevant it’s at what point the £ or $ becomes relevant.
@Tim: mathematically, the basis for calculating significance on revenue improvement is similar. You simply need to input the mean and standard deviation of revenue and rest of math remains the same. We already do it for revenue tracking feature in VWO: https://vwo.com/blog/revenue-tracking-for-ab-testing/
That looks great and would def. give me a reason to use VWO next time. I have a lot of data at the moment in GWO / Analytics for this test that we’ve run so in this particular instance I’ll need to find a way of calculating that significance with the data I’ve got.
The significance level of the test is not determined by the p-value, nor is it the probability that the null hypothesis is true.
One rejects the null hypothesis when the p-value is less than the significance level alpha, which is often 0.05
The p-value is based on the assumption that a result is the product of chance alone, it therefore cannot also be used to gauge the probability of that assumption being true.
The significance level of a test is a value that should be decided upon by the person interpreting the data before the data are viewed,and is compared against the p-value or any other statistic calculated after the test has been performed.
The real meaning is that the p-value is the chance of obtaining such results if the null hypothesis is true.
Can anybody tell me how to derivate the formula of the Z-Score? I need this formula for my thesis, so it would be good if I could explain the correctness of this formula with mathematical literature. Does anybody now books or any other scientifical papers that describe this forumla?
Thank you very much!
Hey Paras. First off, the information you share is awesome, and I love your service.
I’m trying to get my head around all this and I have a few questions:
1) In this spreadsheet, when calculating the 95% Conversion Rate Limits, you multiply your SE by 1.65. However, in your blog entry “What you really need to know about mathematics of A/B split testing” you say that you need to multiply by 1.96 for calculating the 95% range – What am I missing?
2) I’m curious how this multiplier is calculated, if it’s too complex to explain here, how can I learn?
3) In your blog post “What you really need to know about mathematics of A/B split testing” you suggest that you can use a lack of overlap between the conversion rate limits to show one variation is better than the other. In this spreadsheet however you are using the p-value. Does it really matter which is used?
Thanks!
@Jai. Thanks for your comments:
1) Actually, you spotted an error in the spreadsheet. Thanks for commenting it here. The 95% conversion rate range is actually 90% conversion rate range, and you are right 1.96 corresponds to 95% conversion rate range, not 99%. Thanks to you, we noticed this minor error in conversion rate range calculations (though significance results were unaffected as we directly calculate it from p-value, not conversion rate range). The error in fixed in the latest version of spreadsheeet.
2) It will be difficult to explain the calculator here, but if you want to learn there are some excellent resources on the Internet. You should search for z-test or hypothesis testing of binomial variables.
3) P-value in a way measures the overlap between the distributions. Smaller the p-value, smaller the overlap.
Thanks for getting back to me so fast, and thanks for your comments, things make a lot more sense now :).
Hey, I think there’s also a mistake in the formula for the 90% confidence its SI(OU(p_value0,1); “YES”; “NO”)and I think it should be SI(OU(p_value0,9); “YES”; “NO”)
@Ay: yes, you are correct. We’ve fixed it.
Thanks for this fantastic tool!
How would you use this calculator when looking at a test where revenue, not conversion rate is the determining factor of success?
Specifically – if I was conducting and email messaging test where the determining factor of a success treatment is more revenue (not clicks or sales, but overall revenue). For example – perhaps the treatment generates more clicks, but a lower conversion rate – but overall more revenue. Can I still adapt this calculator to calculate significance?
@Dannie: you use the same formulae, but plugin in real average and standard deviation that you get from revenue figures. For conversion rate, we calculate it using the formula p*(1-p)
Hi Paras,
I looked at the Google Doc version of the spreadsheet, and I think all the [2-sided] conversion rate limits (for example: 5.78% to 7.62% for Control at 90% confidence) are correct, and so are the Z-score and P-value, except that the dimensionless Z-score should be reported as 1.72 (or -1.72 if doing “Variation – Control”) and not as 172.167.
However, the formulas for significance (rows 14-16) are incorrect (assuming you are testing for zero versus non-zero difference in rates from control to variation). For example, for 90% confidence, it should be =IF(OR(p_value0.95),”YES”,”NO”) rather than =IF(OR(p_value0.9),”YES”,”NO”).
Thus for a confidence (100*c)%, the formula should be =IF(OR(p_value( 1 – ((1-c)/2) ),”YES”,”NO”).
With this correction, significances will be row14: YES at 90%, row15: NO at 95%, row16: NO at 99%. Which matches the fact that the Z-score of 1.72 is greater than the 90% cut-off of 1.65, but less than the 95% cut-off of 1.96 & of course less than the 99% cut-off of 2.58.
— Sudhakar
Sorry – my earlier comments appear to be truncated.
The correct significance formula at (100*c)%:
YES if p_value(1 – ((1-c)/2)).
— Sudhakar
The p-value mentioned here (https://vwo.com/ab-split-significance-calculator/) doesnt actually seem to the be the p-value. It seems to be calculating confidence.
For example, in the excel image above the follow values in control (visitors: 2000, conversion: 134), and variation (visitors: 3000, conversion: 165), the p-value is 0.95.
The same values when used in the calculator give a value of 0.043. It therefore needs to referred to as confidence instead of p-value
No, both values are p values, but in the excel file in C18 =(control_p-variation_p) and in the calculator it is (variation_p – control_p).
So in the Excel file, the p value for the given values is 0.957435466 ~ 95.7% and in JS it is 1 – 0.957435466 ~ 0.043 ~ 4.3%
So both is right, though it seems as if the order control_p-variation_p is more common.
Hi Paras, this is a great tool to get statistical confidence in A/B testing. Thank you for sharing!
Just wondering if you have multivariate significance calculator as well? Or can you let me know where I can get it?
I second this request – I am looking for one that tests 4 variables
Hi Paras,
regarding you answer about revenue significance – as far as I know the formula assumes normal distribution. So if the revenue is not normally distributed (which is probably right for most commerce sites), you can’t use this formula. Isn’t that right?
@Yael: yes, you’re right.
This spreadsheet is awesome! Finding confidence intervals in rivals’ tools is increasingly a challenge and this solves the problem beautifully.